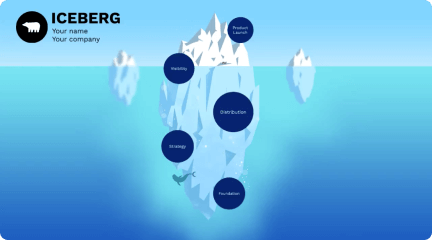
golden ratio
Transcript: Golden Ratio 1.61803399 History Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. But the fascination with the Golden Ratio is not confined just to mathematicians 427-347 BC PLATO 325-265 BC EUCLID 1176-1250 Fibonacci 1445-1517 Pacioli 1571-1630 Kepler 1931 Penrose Mathematics Involved.... ALGEBRAIC Two Quantities are said to be in golden ratio if...... (a+b)/a = a/b= The conjugate root of the previous equation gives us the value of INVERSE GOLDEN RATIO i.e. The number φ turns up frequently in geometry, particularly in figures with pentagonal symmetry. The length of a regular pentagon's diagonal is φ times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles. Triangle whose sides form a geometric progression KEPLER's TRIANGLE The Fibonacci sequence is: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ..... The closed-form expression for the Fibonacci sequence involves the golden ratio: The golden ratio is the limit of the ratios of successive terms of the Fibonacci sequence, as originally shown by Kepler: Aesthetics De Divina Proportione, a three-volume work by Luca Pacioli. He also saw Catholic religious significance in the ratio, which led to his work's title. Containing illustrations of regular solids by Leonardo Da Vinci, Pacioli's longtime friend and collaborator, De Divina Proportione was a major influence on generations of artists and architects alike. Architecture The Parthenon's facade as well as elements of its facade and elsewhere are said by some to be circumscribed by golden rectangles. MAKING GOLDEN RECTANGLE AS PER EUCLID'S ELEMENTA A geometrical analysis of the Great Mosque of Kairouan reveals a consistent application of the golden ratio throughout the design, according to Boussora and Mazouz Art PAINTING Leonardo da Vinci's illustrations of polyhedra in De divina proportione and his views that some bodily proportions exhibit the golden ratio have led some scholars to speculate that he incorporated the golden ratio in his paintings. But the suggestion that his Mona Lisa, for example, employs golden ratio proportions, is not supported by anything in Leonardo's own writings MUSIC James Tenney reconceived his piece For Ann, which consists of up to twelve computer-generated upwardly glissandoing tones, as having each tone start so it is the golden ratio (in between an equal tempered minor and major sixth) below the previous tone, so that the combination tones produced by all consecutive tones are a lower or higher pitch already, or soon to be, produced. NATURE In 2003, Volkmar Weiss and Harald Weiss analyzed psychometric data and theoretical considerations and concluded that the golden ratio underlies the clock cycle of brain waves G OM TRY -1 < r < 2 Odom's construction The 16th-century philosopher Heinrich Agrippa drew a man over a pentagram inside a circle, implying a relationship to the golden ratio. The golden triangle can be characterized as an isosceles triangle ABC with the property that bisecting the angle C produces a new triangle CXB which is a similar triangle to the original. r GOLDEN SPIRAL 2 THANK Continued Fraction ACROPOLIS OF ATHENS Great Mosque of Kairouan 1.6180339557...... 2 Golden relationship with Fibonacci sequence Ptolemy 427-347 interesting mathematical facts..... YOU (1+√5) Therefore, if a Fibonacci number is divided by its immediate predecessor in the sequence, the quotient approximates φ; e.g., 987/610 ≈ 1.6180327868852. These approximations are alternately lower and higher than φ, and converge on φ as the Fibonacci numbers increase Theorem dividing line segment by golden ratio Adolf Zeising, whose main interests were mathematics and philosophy, found the golden ratio expressed in the arrangement of branches along the stems of plants and of veins in leaves. In these phenomena he saw the golden ratio operating as a universal law. If the side lengths of a triangle form a geometric progression and are in the ratio 1 : r : r2, where r is the common ratio, then r must lie in the range φ −1 < r < φ , which is a consequence of the triangle inequality Applications & A pyramid in which the apothem (slant height along the bisector of a face) is equal to φ times the semi-base (half the base width) is sometimes called a golden pyramid 2 Approximate and true golden spirals. The green spiral is made from quarter-circles tangent to the interior of each square, while the red spiral is a Golden Spiral, a special type of logarithmic spiral. Overlapping portions appear yellow. The length of the side of one square divided by that of the next smaller square is the golden ratio. Fibonacci and phi are used in the design of