You're about to create your best presentation ever

Get started with Prezi

Vertex Presentation Template

Create your presentation by reusing one of our great community templates.

VERTEX

Transcript: VERTEX Jahmani Mcclain vertex is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are verticels. information

vertex

Transcript: Geometric perspective makes subjects in a drawing look like they recede into distant space, appearing smaller the farther they are away from you. Skew Lines Parallel Planes Right Prism is a prism that has two bases, one directly above the other, and that has its lateral faces as rectangles. Volume is the amount of 3-dimensional space an object occupies. Capacity. To find the volume of a ellipsoid is: (4/3) pi r1 r2 r3 Prism A solid object that has two identical ends and all flat sides. It can be also a polyhedron. Diagonal In geometry, a polyhedron is a solid in three dimensions with flat faces and straight edges. The area of a cylinder base is: A= Octant Surface Area Lateral Edge skew lines are two lines that do not intersect and are not parallel Lateral Face Oblique Prism A straight line inside a shape that goes from one corner to another (but not an edge). Base The area enclosed by two radius at a 45° angle and the intersected arc. Polyhedron The edge is the lines that form the polygons or a solid In geometry, a dihedral or torsion angle is the angle between two planes that doesn’t form a 90 degrees angle The lateral faces meet to form the lateral edges Dihedral Angle Edge The distance formula is used to determine the distance, d, between two points. The formula to find the distance is: The surface area of a solid object is the total area of the object's faces and curved surfaces. Area of a torus is: A= Perspective Drawing In solid geometric, a face is a flat surface that forms part of the boundary of a solid object Face A oblique prism is a prism with bases that are not aligned one directly above the other The vertex is a venue of the lines to form a polygon like the triangle in the bike Distance Formula Right Prism The faces that join the bases of a solid are called Lateral Faces Any side of a triangle can serve as a base. So any triangle has three bases Volume Parallel planes are the planes that do not intersect. Base Area Vertex

Vertex Presentation

Transcript: Moving Forward This interactive SOP was created to easily train new employees and interns in the solvation process. The solvation SOP is easily accessible to Compound Management as a reference and consistent protocol. As steps change to become more efficient it can be updated with ease. Not only does this make a standard method for processes, it also eliminates the need to ask questions about progression through watching videos and viewing images. The process of solvation is only one procedure out of many that needs to be done consistently by employees to ensure Quality Check. Revising older SOPs can shed light on new techniques that are currently performed to make the process more effective. Standardizing SOPs in all of Vertex can eliminate the simple operating difficulties that occur frequently. This extra time can be used to focus on significant milestones that help us reach our goal of drug discovery. Results Introduction Amir Ali Lipika Agrawal Ana de Guzman Solid compounds are then solvated before getting shipped out to the various locations Discussion The chemists develop the compound A special thanks to: Ben Self Stanley Chan Joe Cohen Alexis Pammit Todd Young 15,000 solid compounds are in the process of being solvated and added to the already existing liquids collection. An updated, interactive SOP for solvation was developed. The compound is then stored in the compound management library The Science of Possibility The Compound Cycle Solvation SOP Scientists can then send orders through the Global Compound Archive(GCA) Compound Management at Vertex There are hundreds of thousands of compounds purchased and synthesized at Vertex that need to be formatted and tracked for assays. Compound Management stores these compounds in environmentally controlled conditions in containers that are registered and tracked in the CMS database. Establishing unified procedures The Compound Management process aims to fulfill requests quickly. Unfortunately, this process consists of numerous protocols that can be handled in many ways, which can cause inconsistent results. The goal of this online instructional presentation serves as a platform to ensure reliable outcomes and train new users. Solvation One of the many protocols done by Compound Management is solvation. This process requires taking a solid compound and dissolving it in dimethyl sulfoxide (DMSO).

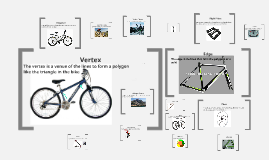
Vertex form presentation

Transcript: Now that we have the vertex, we can use a step pattern to find the next points on the parabola. Every step pattern is originally, (1,3,5,7 etc.) but you need to multiply each step by the value of a if there is one. To use a step pattern, you always move one unit horizontally and then vertically by the value of the step in each direction. Since the a value of this equation is -3, our step pattern is (-3,-9,-15,-21). Vertex form presentation quadratic equations To show how to graph a quadratic equation, I'll use the equation, y=-3(x+7)²-12 as an example. There are two types of quadratic equations; standard form and vertex form. Standard form is ax²+bx+c, but this form isn't easy to get data or graph it. This is why vertex form is useful; in the form a(x - h)²+k, you can easily determine the location of the vertex and find out if the parabola opens up or down or even if it is modified to be more stretched or compressed. To find the vertex, all you need to know is the x-value of the vertex is the same value as h, and the y-value is k. The variable a shows that the parabola was stretched if it's value is >0, or compressed if the value is <0. To see if the parabola opens up or down, simply look to the x²; if it's negative, the parabola opens down and if it's positive it opens up. Now that the parabola is formed, we need to double check to make sure it fits the equation. To do this we can take a point from the parabola, and plug it into the equation to see if it's still correct. I used (-5,-24) and plugged it in: -24=-3(-5+7)²-12 -24=-3(4)-12 -24=-12-12 -24=-24 Since the point fits the equation, we know that it is a point on the parabola. The first step is to find the vertex of the parabola; to do this, you need to identify the x and y values from the equation. Since we know the variable -h= the x-value of the vertex, and -h=7 we can determine that the x of the vertex is -7. The k is equal to the vertex's y-value, so we also know the y value is -12, meaning the vertex= (-7,-12). To graph a parabola Company Logo

Vertex

Transcript: 2a Step 4 Step 5 Step 1 2a Find A,B,&C of f(x)=x +3x-2 Step 2 Step 3 2 Write down the x and y values as an ordered pair & make your graph. __ f(x)=x +3x-2 A____ B____ C____ Split up into groups, no less then 3 people per group & no more than 5. Make a poster about what you learned today. *Give two examples of how to find the vertex Each member must add something. 2 2 Plug into each X to solve. __ f(x)=x +3x-2 Plug -b it in to x f(x)=x +3x-2 Quiz Time! Vertex 2 Group Work Plug in A & B into X= -b

vertex

Transcript: points Y= A(X-H)^2+K 3,0 standard form 3,0 y=ax^2+bx+c a=-.o7 b=.16 c=-2 .38 -2=A(-3-3)^2+0 -2,-3 with the new " formula" the shape changes and shifts to the left. in the first parabola the vertex is one. The second one its more like 2 and weird. 6,- 5 Vertex, domain, range, opening, and axis of symmetry General form x and y intercept 3,0 Y=A(X-3)^2+0 A=-13 -2=A(36) vertex - 2, -5 Y= (-.07)x^2+(.1 6)x+(-2.3) -.78, vertex -7 < x < 7 domain -1<y<10 range axis of symmetry, 0 opening, -2 Equation Nooran Ismail Project 6,-3

vertex

Transcript: reflection Cylinder A solid object with: * two identical flat ends that are circular or elliptical * and one curved side. It has the same cross-section from one end to the other. These hands are congruent An eight sided polygon In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. a symmetrical transformation in which a figure is reversed along an axis so that the new figure produced is a mirror image of the original one octagon 2 dimeneional Vertex A point where two or more straight lines meet. A corner. Example: a corner of a polygon (2D) or of a polyhedron (3D). The plural of vertex is "vertices". Congruent: If one shape can become another using Turns, Flips and/or Slides, then the two shapes are called Congruent: Pair two of something

Vertex

Transcript: Success Story AND part of.. ...INTRIGUED? As you can see, we are a bit creative :) If you think it's not enough, then let's see the digits 20+ years So, the Radio market could be Be creative!!! Dolya & Co. LTD accounting officer BIGGER CFO CAO Rapid, high-quality, reliable communication Design Construction Assembly Installation and maintenance of radio communications service based on the TETRA equipment Zaritskaya Alla CTO Tatarintsev Yaroslav Nibulon Why we are successful? Kyivenergo Protecting shops and shopping centers Security offices, business centers and enterprises Protection of individuals Protection of houses 3000+ Portable radio 50+ Base stations 700+ Mobile radio BIG The security forces Energy companies Agricultural companies Security companies Stadiums, airports Oil and Gas Banks Taxi services EURO 2012 objects modernization of the existing system improving reliability of communication rapid response of emergency crews improved coverage coordination of various services 5 repeaters 5 base radio 100 portable 110 mobile HR Mother Chernobyl radio communication Design and construction License for the design, construction and maintenance of radio equipment Special permission to work with state government services with high confidentiality requirements License to carry out works with cryptographic protection of information шлюз Ukraine Brother Авторизованный дистрибьютор Design, supply, installation of reliable radio communications system based on Vertex Standard radios CMO Vertex Standard №1 in Ukraine Equipping the new car by Vertex Standard radio before Euro 2012: 1000+ mobile radio 500+ portable kits Family then you could imagine much Leader of the Ukrainian telecommunications market Own antennas production The customer is fully satisfied with the performance of the installed system Solved the problem of personnel management Provided a reliable connection throughout and beyond The Chernobyl nuclear power plant Сustomers Security services Specialized licenses Stadiums Main PMR446 Beta-tester Head of the company daughter-in-law Kiev, Ukraine www.dolya.kiev.ua Qality certificate ISO 9001-2001 Certified service center Certified engineers Own antennas production Telecommunications operator License Wide dealers network Thank you for attention! Road Police ALL CEO Cause we are MAFIA Cousine Do you really want to know? MOI 100% coverage of the stadium bowl, underground parking, indoor radio coverage Reliable digital radio Sun Let me introduce my family our company Zaritskaya Alla Tatarintsev Yaroslav Father Our advantages FAMILY! The largest domestic manufacturer and exporter of agricultural products. 43 offices in 11 regions of Ukraine 100% territory coverage 1 repeaters 1 base radio 150 portable 20 mobile Sister-in-law

Explore our templates for more presentation inspiration

Easy Globe Templates for Stunning Presentations | Prezi

Description: For grant requests, program proposals, or any other nonprofit or education presentation, this globe-themed creative Prezi template is the way to generate interest and momentum. Like all Prezi education templates and Prezi nonprofit templates, it’s easy to customize.

Resume

Description: How do you stand out from the stacks of resumes on your prospective employer’s desk? With a Prezi resume template, of course! Create your own “Prezume” and and impress them with your cutting-edge dynamism and cool. All Prezi presentation templates are easy to customize.

Creativity-Paint

Description: For grant requests, funding pitches, program proposals, or any other kind of education or nonprofit presentation, this Prezi template is the way to generate interest and momentum. Like all Prezi education templates and Prezi nonprofit templates, it’s easily customizable.

Report - EDU

Description: If you work in education, make your next report visually interesting and easy to navigate. The line-drawn illustrations in this edu report presentation template encourage curiosity and discovery.

Now you can make any subject more engaging and memorable

Get started with Prezi